Abstract
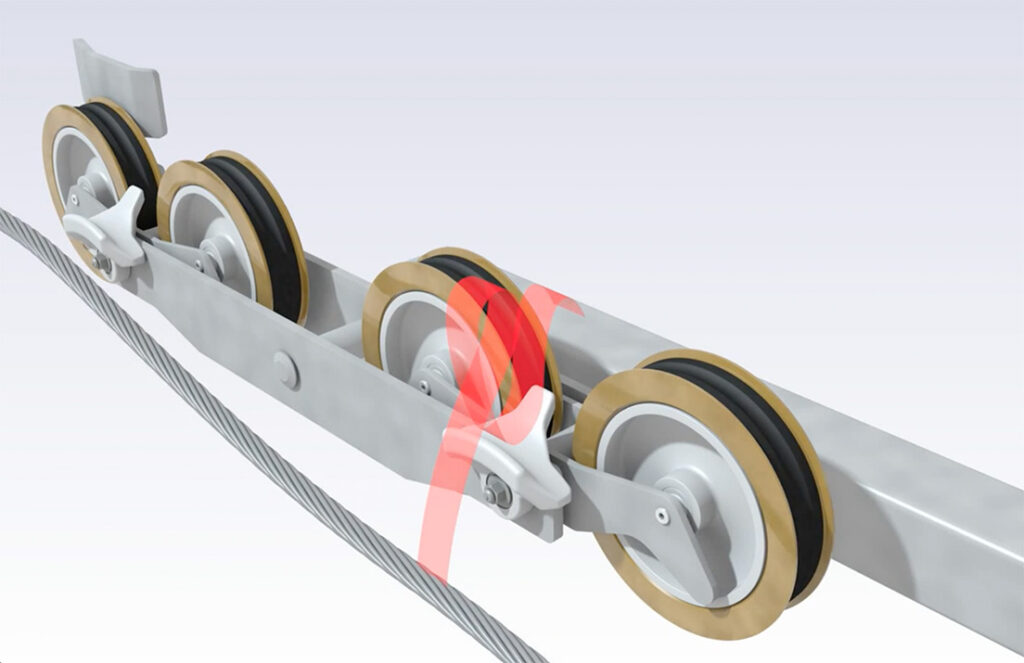
The critical parameters in a rope derailment are the occurring very complex superimposed oscillations of the falling rope and the kinetic energy of the of the total rotating mass.
The cause of suspension rope derailments lies in the constructive interference of rope oscillations of different frequency, phase and direction of propagation. These oscillations can be caused by winds, but also by system faults.
If the oscillation amplitudes at a sheave battery add up, the energy of this oscillation can lift the rope out of the sheaves and even overcome the rope catchers. The kinetic energy of the falling rope introduces additional excitation energy into the system and amplifies the oscillations, which can be propagated over several masts.
Oscillations occurring during a cable derailment
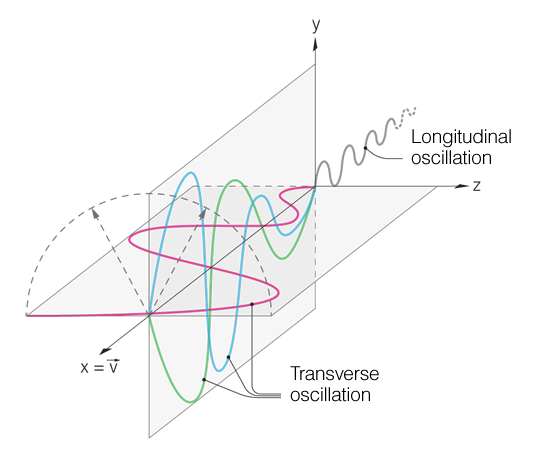
The transverse oscillations
In this type of osillations, the deflection to the direction of propagation is perpendicular to the cable. Each transverse oscillation can consist of different frequencies and phases and exist in different radial directions to the rope. A special form of transverse oscillation is the circular oscillation – such as occurs in the fundamental wave of a skipping rope.
Transverse waves with identical frequency but with a phase shift that is not exactly Π/2 are called elliptical oscillations.
The longitudinal oscillation
In this type of oscillation, the rope is compressed or stretched or relaxed at intervals of the wavelength – i.e. the quotient between the propagation speed and the frequency.
The chair/cabine as a mass pendulum
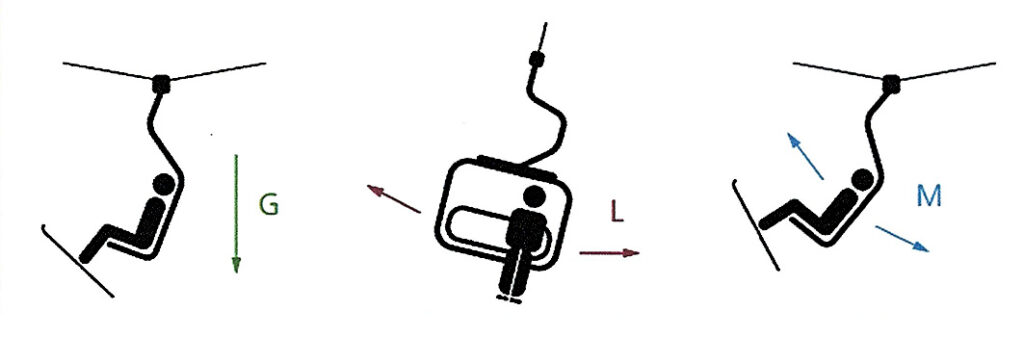
Armchairs with different masses act as multiple pendulums. Here the system is triggered by the braking deceleration. However, the individual chairs/cabine oscillate at different frequencies. They exchange their energies through the rope. The result is a stochastic oscillation in which the amplitudes, oscillation duration and position of energy minima and maxima are unpredictable. Because the rope is subjected to high local forces and force changes per unit of time, transverse waves and circular waves can easily form.
In the event of a derailment, it is important to remove the energy from these oscillations as quickly as possible.
Ekin-total = Ekin-translational + Ekin-rotational + Epotential
In a rope derailment, kinetic energy of over 1.5 MJ can be achieved (1,5 MJ corresponds approximately to the energy released by the detonation of a hand grenade)